Insertion Sort

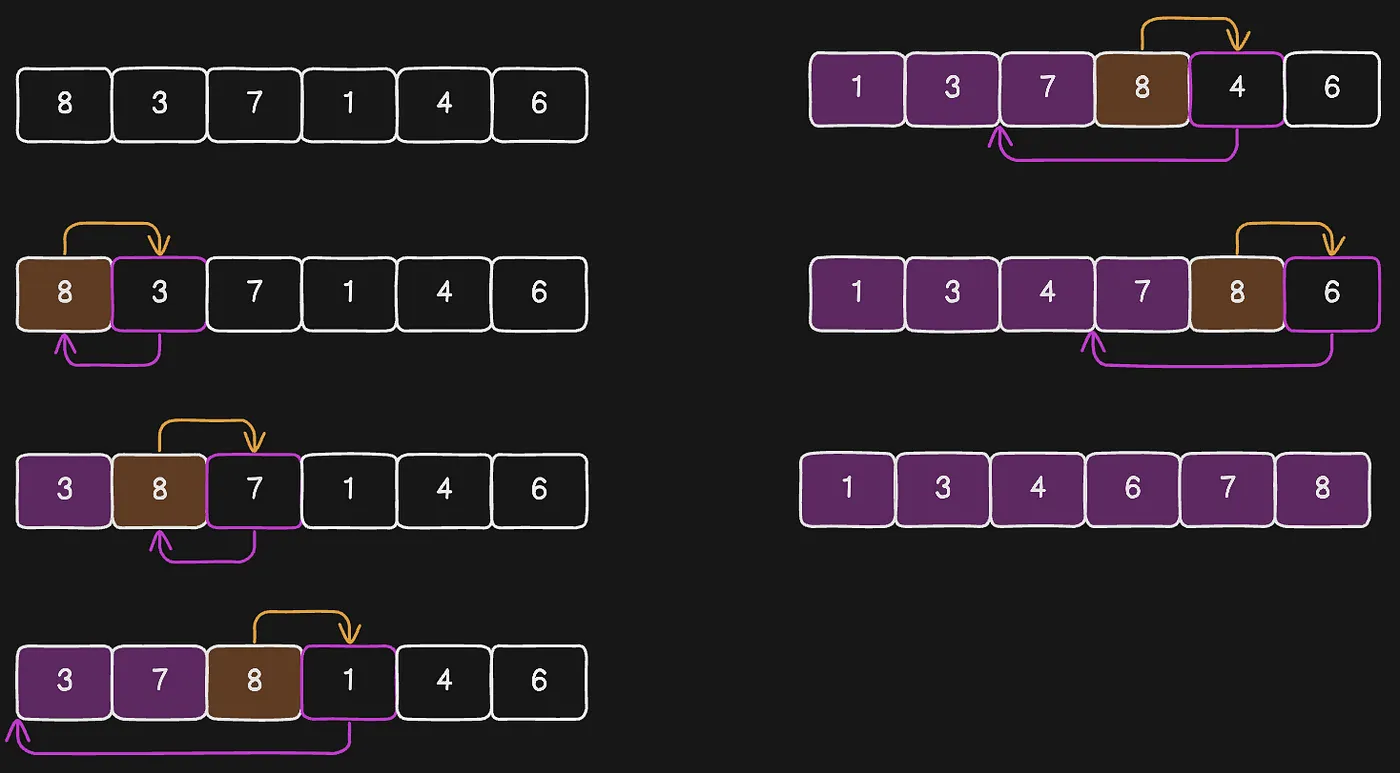
Insertion sort operates much like arranging a hand of cards for a game of poker. You probably would want to rearrange the cards in some order before playing. In most cases, the order is ascending. With this assumption, let’s walk through how we will rearrange the unsorted cards [8, 3, 7, 1, 4, 6].

Beginning with the first card, 8, we compare it with the next card, 3. Since 3 is smaller, we switch their positions, resulting in [3, 8, 7, 1, 4, 6].
Next, we check 8, we find it’s larger than its predecessor, so no changes are needed. The array remains [3, 8, 7, 1, 4, 6].
Next, we examine the third card, 7. Comparing it with the cards to its left (3, 8), we find that it belongs between them. We shift 8 to the right and place 7 in its appropriate position, resulting in[3, 7, 8, 1, 4, 6].
Now the fourth card, 1, is smaller than all the cards to its left. Therefore, we shift all the cards from one position to the right to make room for 1 at the beginning. This results[1, 3, 7, 8, 4, 6].
The fifth card, 4, we can see that it belongs between 3 and 7. So we shift 7 to the right to accommodate 4 in its rightful place, resulting in[1, 3, 4, 7, 8, 6].
Lastly, we examine the sixth card, 6. It’s smaller than 8 but larger than 7. We shift 8 to the right and place 6 in its correct position. The final sorted array is [1, 3, 4, 6, 7, 8].

Let’s use the diagram below I designed to help in visualizing what is happening at each stage.

With a clear understanding of how each step from our card illustration translates into the sorting process, we can now proceed to implement the algorithm in our preferred programming language. I’ll be using JavaScript for demonstration purposes but you can use any language of your choice.

function insertionSort(arr) {
  // Iterate through each element starting from the second one
  // Assume the first element is already sorted
  for (let j = 1; j < arr.length; j++) {
    // Store the current element to be inserted
    let current = arr[j];
    
    // Pointer to keep track of the sorted elements on the left (subarray)
    let i = j - 1;
    
    // Move the current element to its correct position among the sorted elements in the subarray
    while (i >= 0 && arr[i] > current) { // Check if the current element is less than the previous sorted element
      arr[i + 1] = arr[i]; // Shift the previous sorted element to the right
      i--; // Move the pointer to the left to check the next previous sorted element
    }
    
    // Place the current element in its correct sorted position
    arr[i + 1] = current;
  }

  // Return the sorted array
  return arr;
}

Now, the following are the steps and what happens at each stage of the sorting.

Firstly, our initial array: [8, 3, 7, 1, 4, 6]

Iteration 1: key = 3, we compare the key with the elements to its left (8), since 8 is greater than 3, shift 8 to the right by one position resulting array:
[3, 8, 7, 1, 4, 6]
Iteration 2: key = 7, compare key with the elements to its left (8, 3), since 8 is greater than 7, shift 8 to the right by one position resulting array:
[3, 7, 8, 1, 4, 6]
Iteration 3: key = 1, compare key with the elements to its left (8, 7, 3), since all the previous elements are greater than 1, shift 8, 7, and 3 to the right by one position resulting in the array:
[1, 3, 7, 8, 4, 6]
Iteration 4: key = 4, compare key with the elements to its left (8, 7, 3, 1), since all the previous elements are greater than 4, shift 8, 7, 3, and 1 to the right by one position resulting array:
[1, 3, 4, 7, 8, 6]
Iteration 5: key = 6, compare key with the elements to its left (8, 7), since 8 and 7 are greater than 6, shift 8 and 7 to the right by one position resulting array:
[1, 3, 4, 6, 7, 8]
Result: The array is now sorted: [1, 3, 4, 6, 7, 8].

Time Analysis

Worst-Case Scenario (Quadratic Time Complexity — O(n²))

In the worst-case scenario, when the array is completely unsorted, insertion sort results in a quadratic time complexity. This means that the time it takes to sort the array grows quadratically as the size of the array increases.

Each element in the unsorted portion of the array needs to be compared with every element in the sorted portion.
Additionally, if an element from the unsorted portion needs to be inserted into the sorted portion, it may require shifting elements to make space for the new element.
This nested comparison and potential shifting process leads to a quadratic number of operations, proportional to the square of the array size (n²).
So, as the array grows larger, the time taken by insertion sort increases significantly and nonlinearly.

Best-Case Scenario (Linear Time Complexity — O(n))

On the other hand, in the best-case scenario, when the array is already nearly sorted, insertion sort demonstrates linear time complexity.

The number of comparisons and shifts required for each element in the unsorted portion is significantly reduced.
This results in a linear number of operations, directly proportional to the size of the array (n).
Thus, the time taken by insertion sort grows linearly with the size of the array.

Average-Case Scenario

The average-case scenario of insertion sort lies between the best and worst cases.

On average, if elements in the array are randomly ordered, insertion sort tends to perform better than in the worst-case scenario but worse than in the best-case scenario.
The average time complexity is often closer to the worst-case scenario, especially for large input sizes, due to the potential for elements to be positioned in a way that requires more comparisons and shifts.

Understanding these scenarios helps in predicting the performance of insertion sort based on the initial state of the array. In summary, while insertion sort can be efficient for nearly sorted arrays, it may perform significantly slower for highly unsorted arrays.

Latest blogs

Browse all

Merge sort

DSA, Algorithms, Sorting techniques

Algorithms

Sorting

Insertion sort

DSA, Algorithms, Sorting techniques

Algorithms

Sorting

Comparing Running Times with Big O Notation

DSA, Algorithms

Algorithms

Efficiency